Humanities Core Course Spring 2013 Instructor: Bencivenga
LECTURE NOTES
First lecture.
God is for many humans an incomprehensible, unspeakable, but also ineliminable Other (remember Maimonides). And, of course, every human is for me someone else I have to confront, and with whom I have to come to some kind of reconciliation or controversy—and so is any group of humans, any society of them, whether or not I am part of it. The third major Other humans must deal with is the natural world, and through all our civilization the most distinguished and powerful form of encounter with nature has been science. This is true today more than ever, as scientific views and what seems to be their outgrowth—technical gadgets of all sorts—dominate every aspect of our lives. In my lectures I will provide an elementary introduction to the contemporary conception of science, as a prelude to the discussion of other ways of encountering nature (to be carried out later by my fellow lecturers). This introduction will be based on seminal texts that deal with the most central and prestigious of sciences—physics and astronomy, whose conjunction is often referred to as astrophysics. My first text is from the 17th century; my second one was originally published in 1958, and provides a clear account of what is regarded today as the fundamental theory of physical reality. But the reason for considering these two texts together is not merely historical; I will argue that, when ordinary people talk about science, what they are talking about is, most often, still the science of the 17th, or at most the 19th, century. Our common conversation has not yet come to appreciate the radical changes that have occurred within the sciences, and specifically physics, in the 20th century. That is why, hard as it may be, we have to take a look at some of these developments. I cannot expect that you will understand every word of the readings I have assigned; but I consider it important that you struggle with those readings, as such struggle is essential to acquiring any kind of informed, responsible point of view on the natural world as currently understood. And, in any case, I certainly do expect that you will be able to understand every word I say, that is: the specific use I will make here of our texts.
Galileo Galilei (1564-1642) has been regarded by both Albert Einstein and Stephen Hawking as the father of modern science; he is also the first author to give a clear formulation of what has come to be known as the “scientific method.” Therefore, it is natural to have our introduction start with him. In the three lectures I devote to this author and to his Dialogue I will bring out the basic rules of his method and then some of the ways in which the method proves defective. I will make occasional references to passages in the text that are not part of the reading assignments; but all those passages will be quoted here in their entirety and either are self-explanatory or will be explained here. As Galileo’s text consists largely of a comparison of “the two chief world systems” of Ptolemy and Copernicus, I will preface my remarks on that text with a summary of what these systems are.
Begin by considering what the observation of the heavens directly teaches us. First, we see the two “luminaries,” the sun and the moon. The sun rises in the east, sets in the west, and is at its highest daily point in the sky at midday; at that time, it crosses the meridian, that is, the plane identified by the polar axis of the earth and the vertical of the observing place. After sunset, stars appear, now clearly visible against the dark background of the sky, and they follow the same motion as the sun: from east to west. Each night, however, the whole of the starry sky has also traveled a bit toward the west; after one year, the same stars rise again, and the sun has described a complete turn of the starry sky. So a study of the sky, answering questions such as “what star rises just after sunset?”, allows one to locate the season of the year. The solar path in the starry sky is called the zodiac: it is marked by the zodiacal group of stars, or zodiacal constellations. Also, the sun is not always at the same altitude (height) on the horizon, hence its path in the starry sky cannot follow the celestial equator (the projection of the terrestrial equator on the celestial sphere), but is inclined with respect to it at an angle of 23°27'. The great circle it does follow is called the ecliptic, and that intercepts the celestial equator at two points: the vernal and the autumnal equinoxes.
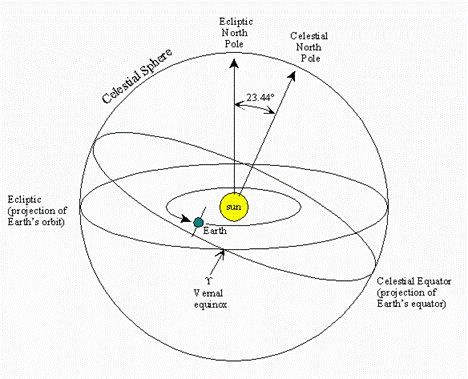
When the sun is in one of those two positions, day and night have equal duration at every point on the earth’s surface. A year can thus be defined in two ways: as the interval between two vernal equinoxes (tropical year) and as the interval between two successive passages of the Sun in front of a given point of the stellar vault (sidereal year). But the two definitions are not equivalent: because (we know now) the axis of the earth rotates in a conical motion with a period of about 26000 years, the direction of the sky where the sun is at the vernal equinox drifts with respect to the stars and describes the complete zodiac; this phenomenon is called the precession of the equinoxes (and, since the constellations were named some 2500 years ago, each sign is now located in a different constellation from the one for which it was originally named).

The tropical year is the one that determines the seasons and is therefore the most important for ordinary life on the earth.
The moon also revolves around the earth (but from west to east), and moves with respect to the stars. It will appear at the same location on the starry background after a sidereal month. During that time, the moon goes through different phases; but in fact the interval between two identical phases (for example, two successive full moons) is slightly longer than the sidereal month (because the phases are determined by the position of the sun, and the sun, too, moves with respect to the stars). Also, the plane on which the moon revolves is not the same as the sun’s. When the moon crosses the plane of the ecliptic, then we can observe an eclipse (and that is the origin of the term “ecliptic”).

Though moving, the stars do not appear to change their reciprocal positions and distances. Other celestial bodies, however, do: they are the planets, or “wandering stars,” which appear in different positions (relative to the stars and to each other) in successive nights. Five of them are visible with the naked eye: Mercury, Venus, Mars, Jupiter, and Saturn. All of them stay very close to the ecliptic; but the motions of the first two (the inner planets) are quite different from those of the others (the outer planets). Mercury and Venus always stay very close to the sun; Mars, Jupiter, and Saturn, on the other hand, move all across the sky. Also, all of them have very irregular motions: mostly they move (like the moon) in a direction opposite to the sun’s (that is, from west to east), but sometimes they are stationary, and sometimes they move in the same direction as the sun (then they are said to have a retrograde motion, or retrogradation).
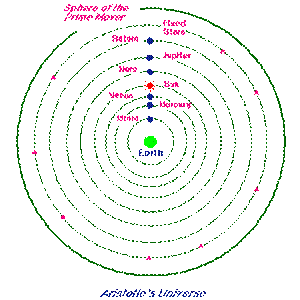
Such are the observational data. With few exceptions, pre-Copernican astronomy explained the data by assuming that the earth was motionless in the center of the universe (that is, by assuming a geocentric model), and that every other celestial body revolved around it—that is, it took the data at face value, and constructed models of increasing complexity to account for what motions in fact took place. We can limit ourselves here to considering (briefly) Aristotle’s and Ptolemy’s contributions to this development. Aristotle believed both the earth and the universe to be spherical—indeed, he took the latter to be constituted by a number of concentric spheres. The four elements earth, water, air, and fire (in this order) belonged for him to the earth’s sphere, and tended to remain in their natural place. Specifically, when they were removed from that place, they tended to return to it; so their natural motions were up and down—down when, say, earth falls toward the center, and up when, say, fire, rises toward the sky. Outside the earth’s sphere were nine others: the moon’s, Mercury’s, Venus’s, the sun’s, Mars’s, Jupiter’s, Saturn’s, the fixed stars, and finally the primum mobile, which transmitted its motion to all other spheres. In contrast with what happens in the sublunar world (the world under the moon), in the heavens there was no generation or corruption: the spheres were made of an incorruptible fifth element (quintessence) called ether, whose natural movement was in a circle that always returned upon itself.
Since the motions of the stars and especially the planets were far more complex than what could be accounted for in terms of the above basic instructions, ancient astronomers had to combine several distinct motions for each celestial body in order to obtain a composite motion that actually fit the data (“saved the phenomena, or appearances”). And all the component motions had to be circular. The two main devices they adopted for this purpose were eccentrics and epicycles, both prominently displayed in the work of the greatest of those astronomers: Ptolemy, who lived in the II century AD and composed the 13 books of the Almagest. An eccentric circle was used to account for the motion of the sun, which was supposed to move on a circle around the earth with a uniform velocity, except that the earth was not at the center of the circle. Epicycles, on the other hand, figured prominently in the account of the motions of the planets: a planet was supposed to move on a circle (the epicycle) whose center in turn moved on another circle, called the deferent circle, around the earth. It can be proved that eccentric models and epicycle models are equivalent; but in the case of the planets, and especially of the inner planets, the two models were combined in order to save the phenomena. The following website gives you some images of how this was supposed to work:
http://abyss.uoregon.edu/~js/glossary/ptolemy.html
Nicholas Copernicus was born in 1473 in
There are three characters in Galileo’s Dialogue (though the author himself is
often evoked as “the Lincean Academician” or “our mutual friend”—see for example pp. 22, 62—and occasionally episodes or
shorter dialogues involving him are reported). Simplicio (who has the same name
as an Aristotelian commentator of the 6th century) is an obstinate
defender of traditional geocentrism; Salviati is Galileo’s spokesman; and
Sagredo is an intelligent and sympathetic interlocutor who lets himself be
convinced of the truth of Copernicus’s and Galileo’s views—often adding
interesting twists and details to the arguments offered by Salviati. The three
characters meet at Sagredo’s palace in
I have thought it most appropriate to explain these concepts in the form of dialogues, which, not being restricted to the rigorous observance of mathematical laws, make room also for digressions which are sometimes no less interesting than the principal argument. (p. 6)
[W]e are arguing for our own amusement, and are not obligated to any such strictness as one would be who was methodically treating a subject for professional reasons, with the intention of publishing it. I do not want this epic of ours to adhere so closely to poetic unity as to leave no room for episodes, for the introduction of which the slightest relevance ought to suffice. It should be almost as if we had met to tell stories, so that it is permitted for me to relate anything which hearing yours may call to my mind. (p. 188)
(But make no mistake about it: Galileo’s dialogue should not be confused with a casual conversation. It is a highly sophisticated and carefully constructed piece of work, and also one that took considerable time—all of six years—to compose.)
Besides offering him great stylistic freedom and being possibly the best format for his intended purpose of popularizing Copernican astronomy, the dialogue form gives Galileo another advantage—though one that, as it turned out, proved ultimately delusive. That is: he does not have to propose and defend such dangerous views in his own name, but can depict himself as the dispassionate observer of a lively debate among others. The execution of Giordano Bruno in 1600 and his own 1616 trial had made considerable impact on Galileo; so through the Dialogue he makes repeated efforts to depict even his characters as espousing heliocentrism only for the sake of argument, as an interesting hypothesis, and the like.
I have taken the Copernican side in the discourse, proceeding as with a pure mathematical hypothesis and striving by every artifice to represent it as superior to supposing the earth motionless…. It is not from failing to take count of what others have thought that we have yielded to asserting that the earth is motionless, and holding the contrary to be a mere mathematical caprice, but (if for nothing else) for those reasons that are supplied by piety, religion, the knowledge of Divine Omnipotence, and a consciousness of the limitations of the human mind (pp. 5-6).
I act the part of Copernicus in our arguments and wear his mask. As to the internal effects upon me of the arguments which I produce in his favor, I want you to be guided not by what I say when we are in the heat of acting out our play, but after I have put off the costume, for perhaps then you shall find me different from what you saw of me on the stage (p. 153).
As I suggested, this ruse proved ineffective. Despite his prudent qualifications, Galileo was tried by the Catholic Inquisition, threatened with torture, and found guilty. It was only as late as 1992 that he was officially rehabilitated by the Catholic Church.